Introduction
Jean-Paul Brasselet, Laurentiu Maxim and Botong Wang will give mini-courses for 3 hours.
Time
July 31--August 2, 2024
Room
5306, the Fifth Teaching Building, East Campus of USTC
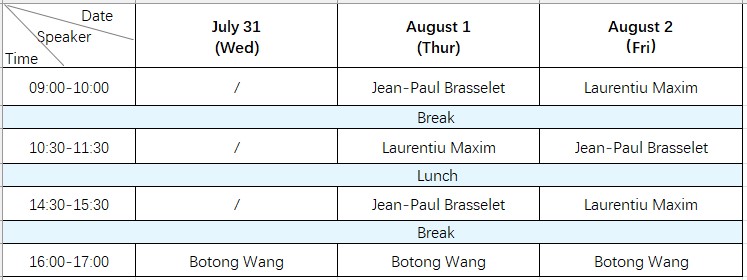
Schedule
Titles and abstracts
 Jean-Paul Brasselet (CNRS)
Jean-Paul Brasselet (CNRS)
Title: Characteristic classes from the origins to the present days.
Abstract: The first part of the course will be a journey through time and space from the very beginning to arrive at the Poincaré-Hopf theorem, the first example of application of the obstruction theory. This theory allows, in the case of real varieties, to define the Stiefel-Whitney classes and also the Wu Wen Tsün (real) classes, which, although less known, are also very useful. We will provide examples of these classes.
In the complex case, the Chern classes, have been defined by Shiing-Shen Chern himself, in many ways, depending on the situation. We will start here with the definition by obstruction theory. That is the way in which they were first generalized to the case of singular varieties.
In 1965 two publications concerning characteristic classes were published without knowing the publicity they would have deserved. In France, Marie-Hélène Schwartz shows that by using "radial'' vector fields we can write a Poincaré-Hopf theorem and construct Chern classes for singular varieties. In China, Wu Wen Tsün defines Chern classes with values in the Chow group of complex projective varieties. In fact the classes thus defined will be rediscovered in a different way in the construction of characteristic classes of Robert MacPherson.
The course will be an opportunity to present theories such as the theory of obstruction mentioned above as well as the stratification theory and the theory of duality, due to Poincaré and which finds here, in the case of singular varieties, a nice application.

Laurentiu Maxim (University of Wisconsin-Madison)
Title: Singularities through the lens of characteristic classes
Lecture 1. Introduction to characteristic classes for singular varieties
Abstract: I will start by introducing characteristic numbers and characteristic classes for singular complex algebraic varieties, with an emphasis on Hirzebruch classes. I will then exploit the Hodge theoretic and motivic nature of the Hirzebruch classes to compute them in several instances, e.g., in the toric context.
Lecture 2. Characteristic classes of hypersurfaces via specialization
Abstract: I will discuss characteristic class theories of Milnor type (e.g., Hirzebruch-Milnor classes) associated with complex hypersurfaces. Such classes measure the complexity of hypersurface singularities, providing vast generalizations of the notion of Milnor number, and they can be described via specialization. Several geometric and topological applications will be also discussed.
Lecture 3. Spectral classes and Applications to rational and du Bois singularities
Abstract: I will make use of the monodromy action to introduce spectral versions of the Hirzebruch-Milnor characteristic classes of hypersurfaces, generalizing the notion of Steenbrink spectrum. I will then explain how these enhanced classes can be used to detect jumping numbers of (higher) multiplier ideals, as well as (higher) du Bois and (higher) rational hypersurface singularities.
 Botong Wang (University of Wisconsin-Madison)
Botong Wang (University of Wisconsin-Madison)
Title: Hodge theory in combinatorial geometry
Abstract: We will give a survey on the recent resolution of two conjectures in matroid theory. The first one is the Heron-Rota-Welsh conjecture by Adiprasito-Huh-Katz, and the second one is the Dowling-Wilson conjecture by Braden-Huh-Matherne-Proudfoot-Wang. The main idea is to attach algebraic geometric invariants to a given matroid, and use ideas from Hodge theory to derive combinatorial properties.
Organizer
Yongqiang Liu (University of Science and Technology of China), liuyq@ustc.edu.cn
Secretary
Chun Tan, nanbei0104@ustc.edu.cn
Organizing Parties
Institute of Geometry and Physics, USTC



